calculo diferencial
lunes, 14 de diciembre de 2015
unidad 5
5.1 Pendiente de la recta tangente a una curva
De un curva que es la gráfica de una función y=f(x), y se p un punto sobre la curva. p es el limite de la pendiente de las rectas que pasan por p y otro punto q sobre la curva cuando se acerca a p.
5.2 Teorema de Rolle
En calculo diferencial, el teorema de Rolle demuestra la existencia de un punto interior en un intervalo abierto para el cual la derivada de una función derivable se anula cuando el valor de ésta en los extremos del intervalo es el mismo. Es generalizado mediante el teorema del valor medio, del que este es un caso especial. Es uno de los principales teoremas en cálculo debido a sus aplicaciones.
Si f es una funcion en la que cumple (i) f es una funcion (ii) f es diferenciable en el intervalo abierto (a,b)
(iii) f (a) =0 y f(b) = 0
5.3 Teorema de valor medio
En cálculo diferencial, el teorema de valor medio (de Lagrange), teorema de los incrementos finitos, teorema de Bonnet-Lagrange o teoría del punto medio es una propiedad de las funciones derivables en un intervalo. Algunos matemáticos consideran que este teorema es el más importante del cálculo (ver también el teorema fundamental del cálculo integral). El teorema no se usa para resolver problemas matemáticos; más bien, se usa normalmente para demostrar otros teoremas. El teorema de valor medio puede usarse para demostrar el teorema de Taylor ya que es un caso especial.
5.4 Criterio de la segunda derivada
El Criterio o prueba de la segunda derivada es un teorema o método del cálculo matemático en el que se utiliza la segunda derivada para efectuar una prueba simple correspondiente a los máximos y mínimos relativos.
Se basa en el hecho de que si la gráfica de una función f es convexa en un intervalo abierto que contiene a f´(c)=0,f(c), y debe ser un mínimo relativo de . De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a f´(c)=0,f(c) y debe ser un máximo relativo de f.
Sea f una función tal que f´(x)=0 y la segunda derivada de existe en un intervalo f abierto que contiene a x.
1. Si f´´(x)>0 , entonces tiene un máximo relativo en .
2. Si f´´(x)<0 , entonces tiene un mínimo relativo en .
1. Si f´(x)=0 , entonces el criterio falla. Esto es,f quizás tenga un máximo relativo en (x,f(x)), un mínimo relativo en o ninguno de los dos. Tomar como ejemplo la función f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.
5.5 Análisis de la variación de funciones
Cuando la variación total de cualquier función particular es finita, en ese caso, esa función se conoce como Función de Variación Acotada, que puede ser abreviada como función BV (Bounded Variation por sus siglas en inglés). El gráfico correspondiente de la función BV se dice entonces que se comporta bien en un sentido preciso. La función BV tiene amplias aplicaciones en el campo de las matemáticas, y es utilizada en algunos de los teoremas más importantes, tal como son los Teoremas de Fourier. En el caso de la funciones continuas que contienen sólo una variable, la variación acotada implica la distancia finita cubierta por un punto a lo largo del eje y. Otra clasificación establece que las funciones de variación acotada, tienen la propiedad de intervalo cerrado, son las funciones que se pueden establecer como la diferencia entre dos monótonas acotadas.
La variación Acotada de una función determinada en el intervalo [x, y] puede ser establecida como
Donde S es el conjunto acotado:
La variación resulta ser infinita si el conjunto no es acotado. El supremo de S puede ser llamado también como Variación Total o sólo la variación de f y se denota como V (f; x, y) o simplemente V (x). Existen ciertos teoremas que pueden ser útiles para el análisis de la variación de la función:
1). Si en el conjunto [x, y], la función está incrementando, en ese caso, es la función de variación acotada en el conjunto [x, y] y consecuentemente V [g [x, y]] = g(y) – g(x).
2). Si en el conjunto [x, y] la función es constante, entonces es la función de variación acotada en el conjunto [x, y] y entonces V [g [x, y]] = 0.
Por ejemplo, la función g(r) = c es una función de variación acotada constante en el intervalo [x, y].
3) En el conjunto [x, y] si, g y f son las funciones de variación acotada y c es constante, en ese caso
a). g es una función de variación acotada en el intervalo [x, y].
b). g es una función de variación acotada en cada subintervalo cerrado del intervalo [x, y].
c). cg es también una función BV en el conjunto [x, y].
d). g + f y g –f son BV en el conjunto [x, y]
e). gf es también BV en el conjunto [x, y].
Algunos datos más útiles acerca de estas funciones especiales se pueden establecer como que una función de variación acotada se puede expresar también por la divergencia de 2 funciones crecientes.
Del mismo modo, todas las funciones totalmente continuas son de naturaleza BV, sin embargo, no es necesario que todas las funciones continuas BV deban ser totalmente continuas.
La función f puede ser considerada como BV en el conjunto [x, y] si, la derivada de f se encuentra acotada en [x, y].
Además, cuando dos funciones variación acotada se multiplican entre sí, entonces la resultante es también una función de variación acotada.
Hay algunas propiedades básicas que son seguidas por las Funciones de Variación Acotada:
1) Las Funciones de Variación Acotada pueden tener discontinuidad de primer tipo, es decir, discontinuidad de salto.
5.6 Problemas de optimización y de tasas relacionadas.
La optimización se refiere al tipo de problema que se ocupa de la determinación de la forma más apropiada para realizar cierta tarea. Con el fin de resolver estos problemas, se calculan los valores mínimos y máximos de la función. Estos incluyen encontrar la distancia mínima para llegar a un punto, el costo mínimo para hacer determinada operación, etc. La función cuyo máximo o mínimo necesita determinase por lo general está sujeta a ciertas restricciones que deben tomarse en cuenta.
Estos problemas son diferentes a los problemas utilizados para encontrar los valores mínimos o máximos locales. Los Problemas de optimización sólo se ocupan de los valores máximos o mínimos que una función puede tomar y no del mínimo o máximo en un intervalo. Es decir, la optimización busca el mínimo o máximo global (absoluto) y no el local. El mínimo o máximo absoluto es el mayor entre el mínimo o máximo local, respectivamente.
Puede haber casos, donde el mínimo o máximo global no existe para una función. En estos el dibujo de la gráfica para la función correspondiente puede ayudar en gran manera.
Hay algunos pasos que deben seguirse con el fin de desglosar un problema de optimización:
1). Lo primero y más importante es identificar las vairables y constantes de la función. Esto ayuda a determinar la parte de la función que será minimizada o maximizada.
2). Escribir la fórmula adecuada para la función particular, para lo cual tenemos que calcular el mínimo o máximo.
3). Ahora, la fórmula será escrita en términos de una sola variable, es decir, f®.
4). Establezca la diferenciación de f® a 0, f ‘® = 0, y resuelva a través de observar todas las limitaciones y otros valores críticos para encontrar los valores extremos.
Por ejemplo, considere la función, g ® = -r2 + 4r – 2. Y siendo el intervalo en el cual el valor máximo será encontrado [0, 1]. Calculando g ‘® se obtiene,
g’ ® = −2r + 4 = 0
Por lo tanto, 2 viene a ser un valor crítico, luego reemplazando el 2 en la función g (2) = 2. Ahora sustituyendo uno por uno los valores del intervalo en el lugar de r, obtenemos,
g (0) = −2 g (1) = 1
Se puede observar, que el valor máximo de g® en [0, 1] es 2.
Un tipo parecido de problema es el problema de las tasas relacionadas. Se trata de un problema en el que se proporciona la tasa de variación de al menos una variable de la función y en el problema se necesita buscar la otra tasa de variación.
También hay ciertas reglas simples para resolver estos problemas:
Considere que f(a) sea una función con dos variables a y b, las cuales cambian con el tiempo y la tasa de variación de a es dada con el tiempo, es decir, dx/dt
1). En primer lugar, encontrar la derivada de f(a), es decir, f ‘(a)
2). Ponga el valor de a en la ecuación
3).Entonces multiplíquelo con dx/dt para obtener dx/dt
Aplicar las reglas en un ejemplo proporcionará una mejor comprensión:
Suponga que la pregunta dada dice lo siguiente: Se está bombeando aire a un globo esférico de 4 cm de radio a 5 cm3 / seg. Entonces, el ritmo de cambio del radio del globo necesita ser calculado.
Se puede observar que el radio y el volumen son las variables de las funciones correspondientes.
dx/dv es dada y es igual a 5 cm3/seg y necesita encontrarse. Como dxr/dv V= 4 r3 / 3.
Diferenciando ambos lados, se obtiene π . Ahora sustituyendo el valor de en esta ecuación, se obtiene dr/dt=7/64π
cm /seg.
Concepto de derivada
En matemática, la derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente. La derivada de una función es un concepto local, es decir, se calcula como el límite de la rapidez de cambio media de la función en un cierto intervalo, cuando el intervalo considerado para la variable independiente se torna cada vez más pequeño. Por ello se habla del valor de la derivada de una cierta función en un punto dado.
En terminología clásica, la diferenciación manifiesta el coeficiente en que una cantidad  cambia a consecuencia de un cambio en otra cantidad
cambia a consecuencia de un cambio en otra cantidad .
.
En matemáticas, coeficiente es un factor multiplicativo que pertenece a cierto objeto como una variable, un vector unitario, una función base, etc.
En física, coeficiente es una expresión numérica que mediante alguna fórmula determina las características o propiedades de un cuerpo.
En nuestro caso, observando la gráfica de la derecha, el coeficiente del que hablamos vendría representado en el punto P de la función por el resultado de la división representada por la relación dy/dx, que como puede comprobarse en la gráfica, es un valor que se mantiene constante a lo largo de la línea recta azul que representa la tangente en el punto P de la función. Esto es fácil de entender puesto que el triángulo rectángulo formado en la gráfica con vértice en el puntoP, por mucho que lo dibujemos más grande, al ser una figura proporcional el resultado de dy/dx es siempre el mismo.
Esta noción constituye la aproximación más veloz a la derivada, puesto que el acercamiento a la pendiente de la recta tangente es tanto por la derecha como por la izquierda de manera simultánea.
Derivadas de orden superior
Sea f(x) una función diferenciable, entonces se dice que f '(x) es la primera derivada de f(x). Puede resultar f '(x) ser una función derivable, entonces podriamos encontrar su segunda derivada, es decir f(x). Mientras las derivadas cumplan ser funciones continuas y que sean derivables podemos encontrar la n-ésima derivada. A estas derivadas se les conoce como derivadas de orden superior.
Ejemplo
Regla l ́hôpital
En matemáticas más específicamente en el calculo diferencial la regla de l'Hôpital o regla de l'Hôpital-Bernoulli1 es una regla que usa derivadas para ayudar a evaluar limite de funciones que estén en forma indeterminada.
Sean f y g dos funciones continuas definidas en el intervalo [a,b], derivables en (a,b) y sea c perteneciente a (a,b) tal que f(c)=g(c)=0 y g'(x)≠0 si x≠c.
Si existe el límite L de f'/g' en c, entonces existe el límite de f/g (en c) y es igual a L. Por lo tanto,
Derivaciones implicitas
Funciones implícitas
Una correspondencia o una función está definida en forma implícita cuando no aparece despejada la y sino que la relación entre x e y viene dada por una ecuación de dos incógnitas cuyo segundo miembro es cero.
Derivadas de funciones implícitas
Para hallar la derivada en forma implícita no es necesario despejar y. Basta derivar miembro a miembro, utilizando las reglas vistas hasta ahora y teniendo presente que:
x'=1.
En general y'≠1.
Por lo que omitiremos x' y dejaremos y'.
lunes, 2 de noviembre de 2015
calculo diferencial limite de una funcion
El límite de una función real de variable real es un concepto fundamental del análisis matemático, un caso de límite que se aplica a otros conceptos de suma importancia como derivada o integral, más aún a las funciones de variable compleja.
Intuitivamente, el hecho que una función f alcance un límite L en el punto c, significa que el valor de f puede ser tan cercano a L como se desee, tomando puntos suficientemente próximos a c, sin importar el valor que pudiera adquirir f en el punto c.
Intuitivamente, el hecho que una función f alcance un límite L en el punto c, significa que el valor de f puede ser tan cercano a L como se desee, tomando puntos suficientemente próximos a c, sin importar el valor que pudiera adquirir f en el punto c.
Funciones de variable real
Si la función  tiene límite
tiene límite  en
en  podemos decir de manera informal que la función
podemos decir de manera informal que la función  tiende hacia el límite
tiende hacia el límite  cerca de
cerca de  si se puede hacer que
si se puede hacer que  esté tan cerca como queramos de
esté tan cerca como queramos de  haciendo que
haciendo que  esté suficientemente cerca de
esté suficientemente cerca de  siendo
siendo  distinto de
distinto de  .
.
 tiene límite
tiene límite  en
en  podemos decir de manera informal que la función
podemos decir de manera informal que la función  tiende hacia el límite
tiende hacia el límite  cerca de
cerca de  si se puede hacer que
si se puede hacer que  esté tan cerca como queramos de
esté tan cerca como queramos de  haciendo que
haciendo que  esté suficientemente cerca de
esté suficientemente cerca de  siendo
siendo  distinto de
distinto de  .
.
Los conceptos cerca y suficientemente cerca son matemáticamente poco precisos. Por esta razón, se da una definición formal de límite que precisa estos conceptos. Entonces se dice:
|
Esto, escrito en notación formal:
Esta formulación estricta del concepto de límite de una función real en un punto de acumulación ( o punto límite) del dominio de la función
continuidad y discontinuidad
De la definición de continuidad se deduce que la gráfica de una función que es continua en un intervalo, es una línea ininterrumpida(es decir, una que se puede trazar sin levantar la pluma o lápiz del papel) sobre el espacio de ese intervalo, o también se hace posible trazar una curva con sólo situar unos pocos puntos y dibujar una línea con trazo ininterrumpido pasando por ellos, se justificará en el caso de varias clases de curvas.
Ejemplos; aplicación de la definición de continuidadEjemplo 1: Demostrar que f(x) = 5 es continua en 7.
Solución: debemos verificar que las tres condiciones se cumplan.
Primera, f (7) = 5, de modo que f está definida en x = 7.
Segunda, por tanto, f tiene limite cuando X —> 7
Tercera, por tanto f es continua en 7
una función es discontinua cuando, una función f definida en un intervalo abierto que contenga aɑ es discontinua en ɑ si:
f no tiene limite cuando x —> ɑ
cuando x —> ɑ, f tiene un límite diferente de f(ɑ)
si f no está definida en ɑ, no es continua allí. Sin embargo, si f no está definida en ɑ pero si está definida para todos los valores cercanos, entonces no solo no es continua en ɑ, es discontinua allí.
Las asíntotas son rectas a las cuales la función se va aproximando indefinidamente, cuando por lo menos una de las variables (x o y) tienden al infinito.
Si un punto (x,y) se desplaza continuamente por una función y=f(x) de tal forma que, por lo menos, una de sus coordenadas tienda al infinito, mientras que la distancia entre ese punto y una recta determinada tiende a cero, esta recta recibe el nombre de asíntota de la función.
 es la asíntota vertical.
es la asíntota vertical.
 es la asíntota horizontal.
es la asíntota horizontal.

 es la asíntota oblicua.
es la asíntota oblicua.
Asíntotas verticales (paralelas al eje OY)
Si existe un número “a” tal, que :
 |
La recta “x = a” es la asíntota vertical.
Ejemplo:
 es la asíntota vertical.
es la asíntota vertical.
Asíntotas horizontales (paralelas al eje OX)
Si existe el límite: :
 |
La recta “y = b” es la asíntota horizontal.
Ejemplo:
 es la asíntota horizontal.
es la asíntota horizontal.
Asíntotas oblicuas (inclinadas)
Si existen los límites: :
 |
La recta “y = mx+n” es la asíntota oblicua.
Ejemplo:

 es la asíntota oblicua.
es la asíntota oblicua.
Suscribirse a:
Comentarios (Atom)























 existe un
existe un 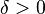 tal que para todo número real x en el dominio de la función
tal que para todo número real x en el dominio de la función  .
.