El límite de una función real de variable real es un concepto fundamental del análisis matemático, un caso de límite que se aplica a otros conceptos de suma importancia como derivada o integral, más aún a las funciones de variable compleja.
Intuitivamente, el hecho que una función f alcance un límite L en el punto c, significa que el valor de f puede ser tan cercano a L como se desee, tomando puntos suficientemente próximos a c, sin importar el valor que pudiera adquirir f en el punto c.
Intuitivamente, el hecho que una función f alcance un límite L en el punto c, significa que el valor de f puede ser tan cercano a L como se desee, tomando puntos suficientemente próximos a c, sin importar el valor que pudiera adquirir f en el punto c.
Funciones de variable real
Si la función  tiene límite
tiene límite  en
en  podemos decir de manera informal que la función
podemos decir de manera informal que la función  tiende hacia el límite
tiende hacia el límite  cerca de
cerca de  si se puede hacer que
si se puede hacer que  esté tan cerca como queramos de
esté tan cerca como queramos de  haciendo que
haciendo que  esté suficientemente cerca de
esté suficientemente cerca de  siendo
siendo  distinto de
distinto de  .
.
 tiene límite
tiene límite  en
en  podemos decir de manera informal que la función
podemos decir de manera informal que la función  tiende hacia el límite
tiende hacia el límite  cerca de
cerca de  si se puede hacer que
si se puede hacer que  esté tan cerca como queramos de
esté tan cerca como queramos de  haciendo que
haciendo que  esté suficientemente cerca de
esté suficientemente cerca de  siendo
siendo  distinto de
distinto de  .
.
Los conceptos cerca y suficientemente cerca son matemáticamente poco precisos. Por esta razón, se da una definición formal de límite que precisa estos conceptos. Entonces se dice:
|
Esto, escrito en notación formal:
Esta formulación estricta del concepto de límite de una función real en un punto de acumulación ( o punto límite) del dominio de la función
continuidad y discontinuidad
De la definición de continuidad se deduce que la gráfica de una función que es continua en un intervalo, es una línea ininterrumpida(es decir, una que se puede trazar sin levantar la pluma o lápiz del papel) sobre el espacio de ese intervalo, o también se hace posible trazar una curva con sólo situar unos pocos puntos y dibujar una línea con trazo ininterrumpido pasando por ellos, se justificará en el caso de varias clases de curvas.
Ejemplos; aplicación de la definición de continuidadEjemplo 1: Demostrar que f(x) = 5 es continua en 7.
Solución: debemos verificar que las tres condiciones se cumplan.
Primera, f (7) = 5, de modo que f está definida en x = 7.
Segunda, por tanto, f tiene limite cuando X —> 7
Tercera, por tanto f es continua en 7
una función es discontinua cuando, una función f definida en un intervalo abierto que contenga aɑ es discontinua en ɑ si:
f no tiene limite cuando x —> ɑ
cuando x —> ɑ, f tiene un límite diferente de f(ɑ)
si f no está definida en ɑ, no es continua allí. Sin embargo, si f no está definida en ɑ pero si está definida para todos los valores cercanos, entonces no solo no es continua en ɑ, es discontinua allí.
Las asíntotas son rectas a las cuales la función se va aproximando indefinidamente, cuando por lo menos una de las variables (x o y) tienden al infinito.
Si un punto (x,y) se desplaza continuamente por una función y=f(x) de tal forma que, por lo menos, una de sus coordenadas tienda al infinito, mientras que la distancia entre ese punto y una recta determinada tiende a cero, esta recta recibe el nombre de asíntota de la función.
 es la asíntota vertical.
es la asíntota vertical.
 es la asíntota horizontal.
es la asíntota horizontal.

 es la asíntota oblicua.
es la asíntota oblicua.
Asíntotas verticales (paralelas al eje OY)
Si existe un número “a” tal, que :
 |
La recta “x = a” es la asíntota vertical.
Ejemplo:
 es la asíntota vertical.
es la asíntota vertical.
Asíntotas horizontales (paralelas al eje OX)
Si existe el límite: :
 |
La recta “y = b” es la asíntota horizontal.
Ejemplo:
 es la asíntota horizontal.
es la asíntota horizontal.
Asíntotas oblicuas (inclinadas)
Si existen los límites: :
 |
La recta “y = mx+n” es la asíntota oblicua.
Ejemplo:

 es la asíntota oblicua.
es la asíntota oblicua.
 existe un
existe un 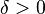 tal que para todo número real x en el dominio de la función
tal que para todo número real x en el dominio de la función  .
.